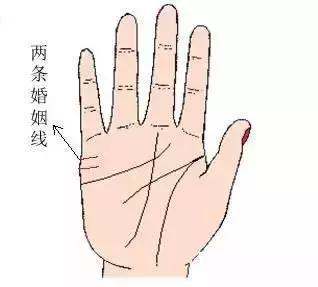
2023年属猴婚姻1980生会离婚吗,属猴和属狗的婚姻如何

属猴2023年会离婚吗?

每年离婚的人都有很多呀，肯定有属猴的，但不能说属猴的一定会在哪一年离婚

1980年属猴2023年运势完整版?

我认为生肖猴聪明伶俐，一向都能够把握自己的运势。而且大多数人性格比较外向，所以说一般都会问一个自己的目标去努力，所以说运势永远掌握在自己手中，所以也不会太差。

属猴女2023年大灾难……会不会离婚?

好好的维持你这段婚姻，婚姻和你的属性也没有什么大的关系，只要两个人感情好，就永远也不会离婚。

80猴2023有一劫难

常州天宁寺的文化不仅是建筑美学和佛学上的千年累积，也是千年来与之相关的名人笔墨须臾不可分的。 清代乾隆皇帝六次下江南，曾三次到天宁寺拈拜，第一次给寺僧颁赐各件，赐给方丈“银牌荷包”，第二次赐给方丈“紫衣”，以示宠贵，第三次除御笔题写“龙城象教”（龙城，常州别称，据清洪亮吉《外家纪闻》记载，每年端午前后，白云溪一带有龙舟竞渡，形成“六龙竞渡白云溪”的盛况。象教亦称像教，为佛家语，就是以形象(或绘佛像或雕佛像)教人,即佛教）匾额外，还为大雄宝殿撰楹联，“合相证三摩，光融西竺；众香超万有，界现南兰”。

1956年属猴是什么命 1956年出生人的命运

不要相信命，相信自己

五六年三月初七酉时出生的男猴的晚年命运如何

[编辑本段]【一、天文学家】

张衡（78-139），东汉建初三年(公元78年)生；永和四年(公元139年)卒。字平子，南阳西鄂（今河南南阳市石桥镇）人，汉族。他是我国东汉时期伟大的天文学家，为我国天文学、机械技术、地震学的发展作出了不可磨灭的贡献；在数学、地理、绘画和文学等方面，张衡也表现出了非凡的才能和广博的学识。

张衡是东汉中期浑天说的代表人物之一；他指出月球本身并不发光，月光其实是日光的反射；他还正确地解释了月食的成因，并且认识到宇宙的无限性和行星运动的快慢与距离地球远近的关系。

张衡观测记录了两千五百颗恒星，创制了世界上第一架能比较准确地表演天象的漏水转浑天仪，第一架测试地震的仪器——候风地动仪，还制造出了指南车、自动记里鼓车、飞行数里的木鸟等等。

张衡共著有科学、哲学、和文学著作三十二篇，其中天文著作有《灵宪》和《灵宪图》等。

为了纪念张衡的功绩，人们将月球背面的一个环形山命名为“张衡环形山”，将小行星1802命名为“张衡小行星”。

20世纪中国著名文学家、历史学家郭沫若对张衡的评价是：“如此全面发展之人物，在世界史中亦所罕见，万祀千龄，令人景仰。”

后世称张衡为木圣（科圣）。

[编辑本段]史书传记

张衡传（出自范晔《后汉书》）

原文：

张衡，字平子，南阳西鄂人也。衡少善属文，游于三辅，因入京师，观太学，遂通五经，贯六艺。虽才高于世，而无骄尚之情。常从容淡静，不好交接欲人。永元中，举孝廉不行，连辟公府不就。时天下承平日久，自王侯以下莫不逾侈。衡乃拟班固《两都》作《二京赋》，因以讽谏。精思傅会，十年乃成。大将军邓骘奇其才，累召不应。

衡善机巧，尤致思于天文阴阳历算。安帝雅闻衡善术学，公车特征拜郎中，再迁为太史令。遂乃研核阴阳，妙尽璇机之正，作浑天仪，著《灵宪》、《算罔论》，言甚详明。

顺帝初，再转复为太史令。衡不慕当世，所居之官辄积好地方额推了我特洛伊特例特二阳台乐而雅而铁路有了年不徙。自去史职，五载复还。

阳嘉元年，复造候风地动仪。以精铜铸成，员径八尺，合盖隆起，形似酒尊，饰以篆文山龟鸟兽之形。中有都柱，傍行八道，施关发机。外有八龙，首衔铜丸，下有蟾蜍，张口承之。其牙机巧制，皆隐在尊中，覆盖周密无际。如有地动，尊则振龙，机发吐丸，而蟾蜍衔之。振声激扬，伺者因此觉知。虽一龙发机，而七首不动，寻其方面，乃知震之所在。验之以事，合契若神。自书典所记，未之有也。尝一龙机发而地不觉动，京师学者咸怪其无征。后数日驿至，果地震陇西，于是皆服其妙。自此以后，乃令史官记地动所从方起。

时政事渐损，权移于下，衡因上疏陈事。……

初，光武善谶，及显宗、肃宗因祖述焉。自中兴之后，儒者争学图纬，兼复附以妖言。衡以图纬虚妄，非圣人之法，乃上疏。……

后迁侍中，帝引在帷幄，讽议左右。尝问衡天下所疾恶者。宦官惧其毁己，皆共目之，衡乃诡对而出。阉竖恐终为其患，遂共谗之。

衡常思图身之事，以为吉凶倚仗，幽微难明。乃作《思玄赋》以宣寄情志。（《思玄赋》略）

永和初，出为河间相。时国王骄奢，不遵典宪；又多豪右，共为不轨。衡下车，治威严，整法度，阴知奸党名姓，一时收禽，上下肃然，称为政理。视事三年，上书乞骸骨，征拜尚书。年六十二，永和四年卒。

著《周官训诂》，崔瑗以为不能有异于诸儒也。又欲继孔子《易》说《彖》、《象》残缺者，竟不能就。所著诗、赋、铭、七言、《灵宪》、《应闲》、《七辩》、《巡诰》、《悬图》凡三十二篇。张衡，字平子，章帝建初三年(公元78年)，诞生于南阳郡西鄂县石桥镇一个破落的官僚家庭(今河南省南阳市城北五十里石桥镇)。祖父张堪是地方官吏，曾任蜀郡太守和渔阳太守。张衡幼年时候，家境已经衰落，有时还要靠亲友的接济。正是这种贫困的生活使他能够接触到社会下层的劳动群众和一些生产、生活实际，从而给他后来的科学创造事业带来了积极的影响。张衡是东汉中期浑天说的代表人物之一；他指出月球本身并不发光，月光其实是日光的反射；他还正确地解释了月食的成因，并且认识到宇宙的无限性和行星运动的快慢与距离地球远近的关系。

[编辑本段]人物生平

张衡出身于名门望族。其祖父张堪自小志高力行，被人称为圣童，曾把家传余财数百万让给他的侄子。光武帝登基后张堪受荐拜官。曾被任为蜀郡太守随大司马吴汉讨伐割据蜀郡的公孙述，立有大功。其后又领兵抗击匈奴有功，拜为渔阳(今北京附近)太守。曾以数千骑兵击破匈奴来犯的一万骑兵。此后在他的任期内匈奴再也没有敢来侵扰。他又教人民耕种，开稻田八千顷，人民由此致富。所以，有民谣歌颂他说：“张君为政，乐不可支。”张堪为官清廉。伐蜀时他是首先攻入成都的，但他对公孙述留下的堆积如山的珍宝毫无所取。蜀郡号称天府，但张堪在奉调离蜀郡太守任时乘的是一辆破车，携带的只有一卷布被囊。

张衡像他的祖父一样，自小刻苦向学，很有文采。16岁以后曾离开家乡到外地游学。他先到了当时的学术文化中心三辅(今陕西西安一带)。这一地区壮丽的山河和宏伟的秦汉古都遗址给他提供了丰富的文学创作素材。以后又到了东汉首都洛阳。在那儿，他进过当时的最高学府——太学，结识了一位青年学者崔瑗，与他结为挚友。崔瑗是当时的经学家、天文学家贾逵的学生，也精通天文、历法、数学等学问。和帝永元十二年(公元100年)张衡应南阳太守鲍德之请，作了他的主簿，掌管文书工作。8年后鲍德调任京师，张衡即辞官居家。在南阳期间他致力于探讨天文、阴阳、历算等学问，并反复研究西汉扬雄著的《太玄经》。他在这些方面的名声引起了汉安帝的注意。永初五年(公元111年)张衡被征召进京，拜为郎中。

元初元年(公元114年)迁尚书郎。次年，迁太史令。以后曾调任他职，但5年后复为太史令。总计前后任此职达14年之久，张衡许多重大的科学研究工作都是在这一阶段里完成的。顺帝阳嘉二年(公元133年)升为侍中。但不久受到宦官排挤中伤，于永和元年(公元136年)调到京外，任河间王刘政的相。刘政是个骄横奢侈、不守中央法典的人，地方许多豪强与他共为不法。张衡到任后严整法纪，打击豪强，使得上下肃然。3年后，他向顺帝上表请求退休，但朝廷却征拜他为尚书。此事颇有蹊跷，因尚书的官职远低于侍中或相，他是否应征，史载不彰。就在这一年(永和四年，即公元139年)他即告逝世。

[编辑本段]学术成就

张衡是一位具有多方面才能的科学家。他的成就涉及到天文学、地震学、机械技术、数学乃至文学艺术等许多领域。

张衡在天文学方面有两项最重要的工作——著《灵宪》，作浑天仪。此外，在历法方面也有所研究。

《灵宪》是张衡有关天文学的一篇代表作，全面体现了张衡在天文学上的成就和发展。原文被《后汉书·天文志》刘昭注所征引而传世。

祖冲之（ZǔChōngzhī ，公元429年—公元500年）是我国杰出的数学家，科学家。南北朝时期人，汉族人，字文远。生于未文帝元嘉六年，卒于齐昏侯永元二年。祖籍范阳郡遒县（今河北涞水县）。先世迁入江南，祖父掌管土木建筑，父亲学识渊博。祖冲之从小接受家传的科学知识。青年时进入华林学省，从事学术活动。一生先后任过南徐州（今镇江市）从事史、公府参军、娄县（今昆山县东北）令、谒者仆射、长水校尉等官职。其主要贡献在数学、天文历法和机械三方面。在数学方面，他写了《缀术》一书，被收入著名的《算经十书》中，作为唐代国子监算学课本，可惜后来失传了。《隋书·律历志》留下一小段关于圆周率（π）的记载，祖冲之算出π的真值在3.1415926（朒数）和3.1415927（盈数）之间，相当于精确到小数第7位，成为当时世界上最先进的成就。这一纪录直到15世纪才由阿拉伯数学家卡西打破。祖冲之还给出π的两个分数形式：22/7（约率）和355/113（密率），其中密率精确到小数第7位，在西方直到16世纪才由荷兰数学家奥托重新发现。祖冲之还和儿子祖暅一起圆满地利用「牟合方盖」解决了球体积的计算问题，得到正确的球体积公式。在天文历法方面，祖冲之创制了《大明历》，最早将岁差引进历法；采用了391年加144个闰月的新闰周；首次精密测出交点月日数（27.21223），回归年日数（365.2428）等数据，还发明了用圭表测量冬至前后若干天的正午太阳影长以定冬至时刻的方法。在机械学方面，他设计制造过水碓磨、铜制机件传动的指南车、千里船、定时器等等。此外，他在音律、文学、考据方面也有造诣，他精通音律，擅长下棋，还写有小说《述异记》。是历史上少有的博学多才的人物。

为纪念这位伟大的古代科学家，人们将月球背面的一座环形山命名为“祖冲之环形山”，将小行星1888命名为“祖冲之小行星”。

祖冲之通过艰苦的努力，他在世界数学史上第一次将圆周率（Л）值计算到小数点后七位，即3.1415926到3.1415927之间。他提出约率22／7和密率355／113，这一密率值是世界上最早提出的，比欧洲早一千多年，所以有人主张叫它“祖率”。他将自己的数学研究成果汇集成一部著作，名为《缀术》，唐朝国学曾经将此书定为数学课本。他编制的《大明历》，第一次将“岁差”引进历法。提出在391年中设置144个闫月。推算出一回归年的长度为365.24281481日，误差只有50秒左右。他不仅是一位杰出的数学家和天文学家，而且还是一位杰出的机械专家。重新造出早已失传的指南车、千里船等巧妙机械多种。此外，他对音乐也有研究。著作有《释论语》、《释孝经》、《易义》、《老子义》、《庄子义》及小说《述异记》等，均早已遗失。

[编辑本段]【人物生平】

从公元42O年东晋灭亡到589年隋朝统一全国的一百七十年中间，我国历史上形成了南北对立的局面，这一时期称作南北朝。南朝从公元42O年东晋大将刘裕夺取帝位，建立宋政权开始，经历了宋、齐、梁、陈四个朝代。同南朝对峙的是北朝，北朝经历了北魏、东魏、西魏，北齐、北周等朝代。祖冲之是南朝人，出生在宋，死的时候已是南齐时期了。

当时由于南朝社会比较安定，农业和手工业都有显著的进步，经济和文化得到了迅速发展，从而也推动了科学的前进。因此，在这一段时期内，南朝出现了一些很有成就的科学家，祖冲之就是其中最杰出的人物之一。

祖冲之的原籍是范阳郡遒县（今河北涞水县）。在西晋末年，祖家由于故乡遭到战争的破坏，迁到江南居住。祖冲之的祖父祖昌，曾在宋朝里担任过大匠卿，负责主持建筑工程，是掌握了一些科学技术知识的；同时，祖家历代对于天文历法都很有研究。因此祖冲之从小就有接触科学技术的机会。

祖冲之对于自然科学和文学、哲学都有广泛的兴趣，特别是对天文、数学和机械制造，更有强烈的爱好和深入的钻研。早在青年时期，他就有了博学多才的名声，并且被派到当时的一个学术研究机关——华林学省，去做研究工作。后来他又担任过地方官职。公元461年，他任南徐州（今江苏镇江）刺史府里的从事。464年，宋朝调他到娄县（今江苏昆山县东北）作县令。

祖冲之在这一段期间，虽然生活很不安定，但是仍然继续坚持学术研究，并且取得了很大的成就。他研究学术的态度非常严谨。他十分重视古人研究的成果，但又决不古人。用他自己的话来说，就是：决不“虚推（盲目崇拜）古人”，而要“搜炼古今（从大量的古今著作中吸取精华）”。一方面，他对于古代科学家刘歆〔xin欣〕、张衡、阚〔kan看〕泽、刘徽、刘洪等人的著述都作了深入的研究，充分吸取其中一切有用的东西。另一方面，他又敢于大胆怀疑前人在科学研究方面的结论，并通过实际观察和研究，加以修正补充，从而取得许多极有价值的科学成果。在天文历法方面，他所编制的《大明历》，是当时最精密的历法。在数学方面，他推算出准确到六位小数的圆周率，取得了当时世界上最优秀的成绩。

宋朝末年，祖冲之回到建康（今南京），担任谒者仆射的官职。从这时起，一直到齐朝初年，他花了较大的精力来研究机械制造，重造指南车，发明千里船、水碓磨等等，作出了出色的贡献。

当祖冲之晚年的时候，齐朝统治集团发生了内乱，腐败黑暗，人民生活非常痛苦。北朝的魏乘机发大兵向南进攻。

从公元494年到5O0年间，江南一带又陷入战火。对于这种内忧外患重重逼迫的局面，祖冲之非常关心。大约在公元494年到498年之间，他担任长水校尉的官职。当时他写了一篇《安边论》，建议开垦荒地，发展农业，增强国力，安定民生，巩固国防。齐明帝看到了这篇文章，打算派祖冲之巡行四方，兴办一些有利于国计民生的事业。但是由于连年战争，他的建议始终没有能够实现。过不多久，这位卓越的大科学家活到七十二岁，就在公元50O年的时候去世了。

改革历法 引入岁差

我国古代劳动人民，由于畜牧业和农业生产的需要，经过长时期的观察，发现了日月运行的基本规律。他们把第一次月圆或月缺到第二次月圆或月缺的一段时间规定为一个月，每个月是二十九天多一点，十二个月称为一年。这种计年方法叫做阴历。他们又观察到：从第一个冬至到下一个冬至（实际上就是地球围绕太阳运行一周的时间）共需要三百六十五天又四分之一天，于是也把这一段时间称作一年。按照这种办法推算的历法通常叫做阳历。但是，阴历一年和阳历一年的天数，并不恰好相等。按照阴历计算，一年共计三百五十四天；按照阳历计算，一年应为三百六十五天五小时四十八分四十六秒。阴历一年比阳历一年要少十一天多。为了使这两种历法的天数一致起来，就必须想办法调整阴历一年的天数。对于这个问题，我们的祖先很早就找到了解决的办法，就是采用“闰月”的办法。在若干年内安排一个闰年，在每个闰年中加入一个闰月。每逢闰年，一年就有十三个月。由于采用了这种闰年的办法，阴历年和阳历年就比较符合了。

在古代，我国历法家一向把十九年定为计算闰年的单位，称为“一章”，在每一章里有七个闰年。也就是说，在十九个年头中，要有七个年头是十三个月。这种闰法一直采用了一千多年，不过它还不够周密、精确。公元412年，北凉赵厞创作《元始历》，才打破了岁章的限制，规定在六百年中间插入二百二十一个闰月。可惜赵厞的改革没有引起当时人的注意，例如著名历算家何承天在公元443年制作《元嘉历》时，还是采用十九年七闰的古法。

祖冲之吸取了赵厞的先进理论，加上他自己的观察，认为十九年七闰的闰数过多，每二百年就要差一天，而赵厞六百年二百二十一闯的闰数却又嫌稍稀，也不十分精密。因此，他提出了三百九十一年内一百四十四闰的新闰法。这个闰法在当时算是最精密的了。

除了改革闰法以外，祖冲之在历法研究上的另一重大成就，是破天荒第一次应用了“岁差。”

根据物理学原理，刚体在旋转运动时，假如丝毫不受外力的影响，旋转的方向和速度应该是一致的；如果受了外力影响，它的旋转速度就要发生周期性的变化。地球就是一个表面凹凸不平、形状不规则的刚体，在运行时常受其他星球吸引力的影响，因而旋转的速度总要发生一些周期性的变化，不可能是绝对均匀一致的。因此，每年太阳运行一周（实际上是地球绕太阳运行一周），不可能完全回到上一年的冬至点上，总要相差一个微小距离。按现在天文学家的精确计算，大约每年相差50.2秒，每七十一年八个月向后移一度。这种现象叫作岁差。

随着天文学的逐渐发展，我国古代科学家们渐渐发现了岁差的现象。西汉的邓平、东汉的刘歆、贾逵等人都曾观测出冬至点后移的现象，不过他们都还没有明确地指出岁差的存在。到东晋初年，天文学家虞喜才开始肯定岁差现象的存在，并且首先主张在历法中引入岁差。他给岁差提出了第一个数据，算出冬至日每五十年退后一度。后来到南朝宋的初年，何承天认为岁差每一百年差一度，但是他在他所制定的《元嘉历》中并没有应用岁差。

祖冲之继承了前人的科学研究成果，不但证实了岁差现象的存在，算出岁差是每四十五年十一个月后退一度，而且在他制作的《大明历》中应用了岁差。因为他所根据的天文史料都还是不够准确的，所以他提出的数据自然也不可能十分准确。尽管如此，祖冲之把岁差应用到历法中，在天文历法史上却是一个创举，为我国历法的改进揭开了新的一页。到了隋朝以后，岁差已为很多历法家所重视了，像隋朝的《大业历》、《皇极历》中都应用了岁差。

祖冲之在历法研究方面的第三个巨大贡献，就是能够求出历法中通常称为“交点月”的日数。

所谓交点月，就是月亮连续两次经过“黄道”和“白道”的交叉点，前后相隔的时间。黄道是指我们在地球上的人看到的太阳运行的轨道，白道是我们在地球上的人看到的月亮运行的轨道。交点月的日数是可以推算得出来的。祖冲之测得的交点月的日数是27.21223日，比过去天文学家测得的要精密得多，同近代天文学家所测得的交点月的日数27.21222日已极为近似。在当时天文学的水平下，祖冲之能得到这样精密的数字，成绩实在惊人。

由于日蚀和月蚀都是在黄道和白道交点的附近发生，所以推算出交点月的日数以后，就更能准确地推算出日蚀或月蚀发生的时间。祖冲之在他制订的《大明历》中，应用交点月推算出来的日、月蚀时间比过去准确，和实际出现日、月蚀的时间都很接近。

祖冲之根据上述的研究成果，终于成功制成了当时最科学、最进步的历法——《大明历》。这是祖冲之科学研究的天才结晶，也是他在天文历法上最卓越的贡献。

此外，祖冲之对木、水、火、金、土等五大行星在天空运行的轨道和运行一周所需的时间，也进行了观测和推算。我国古代科学家算出木星（古代称为岁星）每十二年运转一周。西汉刘歆作《三统历》时，发现木星运转一周不足十二年。祖冲之更进一步，算出木星运转一周的时间为11．858年。现代科学家推算木星运行的周期约为 11. 862年。祖冲之算得的结果，同这个数字仅仅相差0.04年。此外，祖冲之算出水星运转一周的时间为115.88日，这同近代天文学家测定的数字在两位小数以内完全一致。他算出金星运转一周的时间为583.93日，同现代科学家测定的数字仅差0.01日。

公元462年（宋大明六年），祖冲之把精心编成的《大明历》送给，请求公布实行。宋孝武帝命令懂得历法的官员对这部历法的优劣进行讨论。在讨论过程中，祖冲之遭到了以戴法兴为代表的守旧的反对。戴法兴是宋孝武帝的亲信大臣，很有权势。由于他带头反对新历，朝廷大小官员也随声附和，大家不赞成改变历法。

祖冲之为了坚持自己的正确主张，理直气壮地同戴法兴展开了一场激烈的辩论。

这一场关于新历法优劣的辩论，实际上反映了当时科学和反科学、进步和保守两种的尖锐斗争。戴法兴首先上书皇帝，从古书中抬出古圣先贤的招牌来压制祖冲之。他说，冬至时的太阳总在一定的位置上，这是古圣先贤测定的，是万世不能改变的。他说，祖冲之以为冬至点每年有稍微移动，是诬蔑了天，违背了圣人的经典。是一种大逆不道的行为。他又把当时通行的十九年七闰的历法，也说是古圣先贤所制定，永远不能更改。他甚至骂祖冲之是浅陋的凡夫俗子，没有资格谈改革历法。

祖冲之对权贵的攻击丝毫没有惧色。他写了一篇有名的驳议。他根据古代的文献记载和当时观测太阳的记录，证明冬至点是有变动的。他指出：事实十分明白，怎么可以信古而疑今。他又详细地举出多年来亲自观测冬至前后各天正午日影长短的变化，精确地推算出冬至的日期和时刻，从此说明十九年七闰是很不精密的。他责问说：“旧的历法不精确，难道还应当永远用下去，永远不许改革？谁要说《大明历》不好，应当拿出确凿的证据来。如果有证据，我愿受过。”

当时戴法兴指不出新历到底有哪些缺点，于是就争论到日行快慢、日影长短、月行快慢等等问题上去。祖冲之一项一项地据理力争，都驳倒了他。

在祖冲之理直气壮的驳斥下，戴法兴没话可以答辩了，竟蛮不讲理地说：“新历法再好也不能用。”祖冲之并没有被戴法兴这种蛮横态度吓倒，却坚决地表示：“决不应该盲目古人。既然发现了旧历法的缺点，又确定了新历法有许多优点，就应当改用新的。”

在这场大辩论中，许多大臣被祖冲之精辟透彻的理论说服了，但是他们因为畏惧戴法兴的权势，不敢替祖冲之说话。最后有一个叫巢尚之的大臣出来对祖冲之表示支持。他说《大明历》是祖冲之多年研究的成果，根据《大明历》来推算元嘉十三年（436）、十四年（437）、二十八年（451）、大明三年（459）的四次月蚀都很准确，用旧历法推算的结果误差就很大，《大明历》既然由事实证明比较好，就应当采用。

这样一来，戴法兴只有哑口无言。祖冲之取得了最后胜利。宋孝武帝决定在大明九年（465）改行新历。谁知大明八年孝武帝死了，接着统治集团内发生变乱，改历这件事就被搁置起来。一直到梁朝天监九年（51O），新历才被正式采用，可是那时祖冲之已去世十年了。

圆周定律 著书缀术

祖冲之不但精通天文、历法，他在数学方面的贡献，特别对“圆周率”研究的杰出成就，更是超越前代，在世界数学史上放射着异彩。

我们都知道圆周率就是圆的周长和同一圆的直径的比，这个比值是一个常数，现在通用希腊字母“π”来表示。圆周率是一个永远除不尽的无穷小数，它不能用分数、有限小数或循环小数完全准确地表示出来。由于现代数学的进步，已计算出了小数点后两千多位数字的圆周率。

圆周率的应用很广泛。尤其是在天文、历法方面，凡牵涉到圆的一切问题，都要使用圆周率来推算。我国古代劳动人民在生产实践中求得的最早的圆周率值是“ 3”，这当然很不精密，但一直被沿用到西汉。后来，随着天文、数学等科学的发展，研究圆周率的人越来越多了。西汉末年的刘歆首先抛弃“3”这个不精确的圆周率值，他曾经采用过的圆周率是3.547。东汉的张衡也算出圆周率为π=3.1622。这些数值比起π=3当然有了很大的进步，但是还远远不够精密。到了三国末年，数学家刘徽创造了用割圆术来求圆周率的方法，圆周率的研究才获得了重大的进展。

用割圆术来求圆周率的方法，大致是这样：先作一个圆，再在圆内作一内接正六边形。假设这圆的直径是2，那么半径就等于1。内接正六边形的一边一定等于半径，所以也等于1；它的周长就等于6。如果把内接正六边形的周长6当作圆的周长，用直径2去除，得到周长与直径的比π=6/2=3，这就是古代π=3的数值。但是这个数值是不正确的，我们可以清楚地看出内接正六边形的周长远远小于圆周的周长。

如果我们把内接正六边形的边数加倍，改为内接正十二边形，再用适当方法求出它的周长，那么我们就可以看出，这个周长比内按正六边形的周长更接近圆的周长，这个内接正十二边形的面积也更接近圆面积。从这里就可以得到这样一个结论：圆内所做的内接正多边形的边数越多，它各边相加的总长度（周长）和圆周周长之间的差额就越小。从理论上来讲，如果内接正多边形的边数增加到无限多时，那时正多边形的周界就会同圆周密切重合在一起，从此计算出来的内接无限正多边形的面积，也就和圆面积相等了。不过事实上，我们不可能把内接正多边形的边数增加到无限多，而使这无限正多边形的周界同圆周重合。只能有限度地增加内接正多边形的边数，使它的周界和圆周接近重合。所以用增加圆的内接正多边形边数的办法求圆周率，得数永远稍小于π的真实数值。刘徽就是根据这个道理，从圆内接正六边形开始，逐次加倍地增加边数，一直计算到内接正九十六边形为止，求得了圆周率是3.141024。把这个数化为分数，就是157/50。刘徽所求得的圆周率，后来被称为“徽率”。他这种计算方法，实际上已具备了近代数学中的极限概念。这是我国古代关于圆周率的研究的一个光辉成就。

祖冲之在推求圆周率方面又获得了超越前人的重大成就。根据《隋书·律历志》的记载，祖冲之把一丈化为一亿忽，以此为直径求圆周率。他计算的结果共得到两个数：一个是盈数（即过剩的近似值），为3.1415927；一个是朒数（即不足的近似值），为3.1415926。圆周率真值正好在盈朒两数之间。《隋书》只有这样简单的记载，没有具体说明他是用什么方法计算出来的。不过从当时的数学水平来看，除刘徽的割圆术外，还没有更好的方法。祖冲之很可能就是采用了这种方法。因为采用刘徽的方法，把圆的内接正多边形的边数增多到24576边时，便恰好可以得出祖冲之所求得的结果。